Modelo de Bohr.. ( Facundo Garcia,Pablo Velichco,Agustin Abalo,Rodrigo Ramos, Mateo Ojeda)
El modelo atómico de Bohr o de Bohr-Rutherford es un modelo
clásico del átomo, pero fue el primer modelo atómico en el que se introduce una
cuantización a partir de ciertos postulados (ver abajo). Fue
propuesto en 1913 por el físico danés Niels Bohr, para explicar cómo los electrones pueden tener órbitas estables alrededor
del núcleo y por qué los
átomos presentaban espectros de emisión característicos (dos problemas que eran
ignorados en el modelo previo de Rutherford). Además el modelo de Bohr
incorporaba ideas tomadas del efecto fotoeléctrico,
explicado por Albert Einstein en 1905.
Bohr
se basó en el átomo de hidrógeno para hacer el modelo que lleva
su nombre. Bohr intentaba realizar un modelo atómico capaz de explicar la
estabilidad de la materia y los espectros de emisión y absorción discretos que
se observan en los gases. Describió el átomo de hidrógeno con un protón en el núcleo, y girando a su alrededor un electrón. El
modelo atómico de Bohr partía conceptualmente del modelo atómico de Rutherford
y de las incipientes ideas sobre cuantización que habían surgido unos años
antes con las investigaciones de Max Planck y Albert Einstein.
En 1913
Bohr publicó una explicación teórica para el espectro atómico del hidrógeno.
Basándose en las ideas previas de Max Plank, que en 1900 había elaborado una teoría sobre la discontinuidad de la energía (Teoría de los cuantos), Bohr supuso que el átomo solo puede tener ciertos niveles de energía definidos. Bohr establece así, que los electrones solo pueden girar en ciertas órbitas de radios determinados. Estas órbitas son estacionarias, en ellas el electrón no emite energía: la energía cinética del electrón equilibra exactamente la atracción electrostática entre las cargas opuestas de núcleo y electrón. El electrón solo puede tomar así los valores de energía correspondientes a esas órbitas. Los saltos de los electrones desde niveles de mayor energía a otros de menor energía o viceversa suponen, respectivamente, una emisión o una absorción de energía electromagnética (fotones de luz). |


Bohr unió la idea de átomo nuclear de Rutherford con las ideas de una nueva rama de la Ciencia: la Física Cuántica. Así, en 1913 formuló una hipótesis sobre la estructura atómica en la que estableció tres postulados:
¤ El electrón no puede girar en cualquier órbita, sino sólo en un cierto número de órbitas estables. En el modelo de Rutherford se aceptaba un número infinito de órbitas.
¤ Cuando el electrón gira en estas órbitas no emite energía.
¤ Cuando un átomo estable sufre una interacción, como puede ser el imapacto de un electrón o el choque con otro átomo, uno de sus electrones puede pasar a otra órbita estable o ser arrancado del átomo.
¤ El electrón no puede girar en cualquier órbita, sino sólo en un cierto número de órbitas estables. En el modelo de Rutherford se aceptaba un número infinito de órbitas.
¤ Cuando el electrón gira en estas órbitas no emite energía.
¤ Cuando un átomo estable sufre una interacción, como puede ser el imapacto de un electrón o el choque con otro átomo, uno de sus electrones puede pasar a otra órbita estable o ser arrancado del átomo.
El átomo de hidrógeno según el modelo atómico de Bohr
¤ El átomo de hidrógeno tiene un núcleo con un protón.
¤ El átomo de hidrógeno tiene un electrón que está girando en la primera órbita alrededor del núcleo. Esta órbita es la de menor energía.
¤ Si se le comunica energía a este electrón, saltará desde la primera órbita a otra de mayor energía. cuando regrese a la primera órbita emitirá energía en forma de radiación luminosa.
¤ El átomo de hidrógeno tiene un núcleo con un protón.
¤ El átomo de hidrógeno tiene un electrón que está girando en la primera órbita alrededor del núcleo. Esta órbita es la de menor energía.
¤ Si se le comunica energía a este electrón, saltará desde la primera órbita a otra de mayor energía. cuando regrese a la primera órbita emitirá energía en forma de radiación luminosa.
Primer postulado
Los electrones describen órbitas circulares en torno al núcleo del átomo sin irradiar energía.La causa de que el electrón no irradie energía en su órbita es, de momento, un postulado, ya que según la electrodinámica clásica una carga con un movimiento acelerado debe emitir energía en forma de radiación.
Para conseguir el equilibrio en la órbita circular, las dos fuerzas que siente el electrón: la fuerza coulombiana, atractiva, por la presencia del núcleo y la fuerza centrífuga, repulsiva por tratarse de un sistema no inercial, deben ser iguales en magnitud en toda la órbita. Esto nos da la siguiente expresión:
- Donde el primer término es la fuerza eléctrica o de Coulomb, y el segundo es la fuerza centrífuga; k es la constante de la fuerza de Coulomb, Z es el número atómico del átomo, e es la carga del electrón,
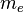 es la masa del electrón, v es la velocidad del electrón en la órbita y r el radio de la órbita.
es la masa del electrón, v es la velocidad del electrón en la órbita y r el radio de la órbita.
Y ahora con ésta ecuación y sabiendo que la energía total es la suma de las energías cinética y potencial:
- Donde queda expresada la energía de una órbita circular para el electrón en función del radio de dicha órbita.
Segundo postulado
No toda órbita para electrón está permitida, tan solo se puede encontrar en órbitas cuyo radio cumpla que el momento angular, , del electrón sea un múltiplo entero de
, del electrón sea un múltiplo entero de 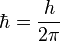 Esta condición matemáticamente se escribe:
Esta condición matemáticamente se escribe:- con
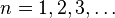
 y queda la condición de cuantización para los radios permitidos:
y queda la condición de cuantización para los radios permitidos:- con
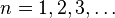 ;
subíndice introducido en esta expresión para resaltar que el radio
ahora es una magnitud discreta, a diferencia de lo que decía el primer
postulado.
;
subíndice introducido en esta expresión para resaltar que el radio
ahora es una magnitud discreta, a diferencia de lo que decía el primer
postulado.
 , número cuántico principal, obtenemos los radios de las órbitas permitidas. Al primero de ellos (con n=1), se le llama radio de Bohr:
, número cuántico principal, obtenemos los radios de las órbitas permitidas. Al primero de ellos (con n=1), se le llama radio de Bohr:- expresando el resultado en ångström.
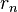 en la expresión para la energía de la órbita y obtener así la energía correspondiente a cada nivel permitido:
en la expresión para la energía de la órbita y obtener así la energía correspondiente a cada nivel permitido:Igual que antes, para el átomo de Hidrógeno (Z=1) y el primer nivel permitido (n=1), obtenemos:
- que es la llamada energía del estado fundamental del átomo de Hidrógeno.
Tercer postulado
El electrón solo emite o absorbe energía en los saltos de una órbita permitida a otra. En dicho cambio emite o absorbe un fotón cuya energía es la diferencia de energía entre ambos niveles. Este fotón, según la ley de Planck tiene una energía:- donde
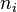 identifica la órbita inicial y
identifica la órbita inicial y 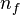 la final, y
la final, y  es la frecuencia.
es la frecuencia.
A veces, en vez de la frecuencia se suele dar la inversa de la longitud de onda:
Ésta última expresión fue muy bien recibida porque explicaba teóricamente la fórmula fenomenológica hallada antes por Balmer para describir las líneas espectrales observadas desde finales del siglo XIX en la desexcitación del Hidrógeno, que venían dadas por:
- con
 , y donde
, y donde 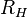 es la constante de Rydberg para el hidrógeno. Y como vemos, la expresión teórica para el caso
es la constante de Rydberg para el hidrógeno. Y como vemos, la expresión teórica para el caso  , es la expresión predicha por Balmer, y el valor medido experimentalmente de la constante de Rydberg (
, es la expresión predicha por Balmer, y el valor medido experimentalmente de la constante de Rydberg ( ), coincide con el valor de la fórmula teórica.
), coincide con el valor de la fórmula teórica.
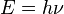 consiguió cuantizar las órbitas observando las líneas del espectro.
consiguió cuantizar las órbitas observando las líneas del espectro.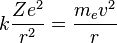



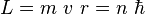




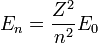

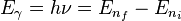




0 Comentarios:
Publicar un comentario
Suscribirse a Comentarios de la entrada [Atom]
<< Página Principal